質量が一様分布である線形ばねの等価質量の導出

ばね質量系では、ばねの質量をゼロとして考えることが一般的です。しかし、実際のばねには質量があります。当然、ばねの長さ方向の位置によって運動速度が異なるため、単純にばねの質量を足すだけでは成り立たちません。そこで、質量のあるばね質量系を、あたかも質量のないばね質量系として等価的に扱うために等価質量という考え方をします。

この記事では、質量が一様分布である線形ばねの等価質量の導出方法を紹介します。

等価質量の導出

以下のような系を考えます。

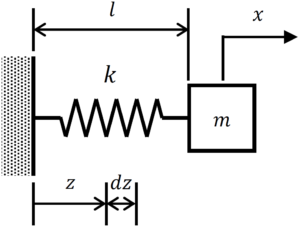
記号	単位	意味
\(l\)	\(\rm m\)	ばねの自然長
\(m\)	\(\rm kg\)	質点の質量
\(M\)	\(\rm kg\)	ばねの質量
\(k\)	\(\rm N/m\)	ばね定数
\(x\)	\(\rm m\)	質点の変位
\(z\)	\(\rm m\)	ばねの固定端座標
\(x_z\)	\(\rm m\)	ばねの位置\(z\)における伸び
\(\rho\)	\(\rm kg/m\)	ばねの単位長さあたりの質量

仮定

1. ばねの質量分布が一様であることです。つまり、ばねの単位長さあたりの質量\(\rho\)がばねの長さ方向\(z\)に依らないです。
2. 線形ばねであることです。つまり、ばねは変位に比例した力を発生させます。フックの法則\(F=kx\)が成り立ちます。

導出

方針として、質量のあるばねの微小な運動エネルギーを求めて積分し、力学的エネルギー保存の法則から等価質量の関係を導きます。

仮定1より、ばねの微小質量は\(dM=\rho dz\)となります。また、ばねの位置\(z\)における伸び\(x_z\)を表したいです。ばね長さ\(l\)で伸びは\(x\)であるから、仮定2より、\(z:x_z=l:x\)です。よって、\(x_z = \displaystyle\frac{z}{l}x\)として表せます。これを時間微分すると、$$\dot{x}_z = \displaystyle\frac{z}{l}\dot{x} \tag{1}$$となります。ここで、微小長さのばねがもつ運動エネルギー\(dK_s\)は、$$ \begin{align} dK_s &= \displaystyle\frac{1}{2}dm\dot{x}_z^2 \\ &=\displaystyle\frac{1}{2}\rho dz \left( \displaystyle\frac{z}{l}\dot{x} \right)^2 \\ &= \displaystyle\frac{1}{2}\rho \left( \displaystyle\frac{\dot{x}}{l} \right)^2 z^2 dz \tag{2} \end{align} $$となります。ばねがもつ全運動エネルギー\(K_s\)は、\(0\)から\(l\)まで積分すれば、$$ \begin{align} K_s &= \displaystyle \int dK_s \\ &= \displaystyle \int_0^{l} \displaystyle\frac{1}{2}\rho \left( \displaystyle\frac{\dot{x}}{l} \right)^2 z^2 dz \\ &= \displaystyle\frac{1}{2}\rho \left( \displaystyle\frac{\dot{x}}{l} \right)^2 \displaystyle \int_0^{l} z^2 dz \\ &= \displaystyle\frac{1}{2} \frac{\rho l}{3}\dot{x}^2 \\ &= \displaystyle\frac{1}{2} \frac{M}{3}\dot{x}^2 \tag{3} \end{align} $$

次に、系全体の力学的エネルギーを考えます。非平衡状態での力学的エネルギー\(E\)は、$$ \begin{align} E &= K + K_s +U \\ &= \displaystyle\frac{1}{2} m\dot{x}^2 + \displaystyle\frac{1}{2} \frac{M}{3}\dot{x}^2 + kx^2 \\ &= \displaystyle\frac{1}{2} \left(m+\frac{M}{3} \right)\dot{x}^2 + kx^2 \tag{4} \end{align} $$となります。すなわち、質量(\(m+\frac{M}{3} \) )が、質量のないばねによって接続されたばね質量系とみなすことができます。

したがって、ばねの等価質量は、ばね質量の\(1/3\)と得られます。

Tips

本結果より、以下の2点のような考察ができると思います。

ばねの質量をゼロと仮定するのは妥当な考え方

今回取り上げたような線形システムにおいて、ばねの質量をゼロと仮定して考えたとしても、最終的に質点の質量に1/3倍したばねの質量を足すだけでよいという結論が導かれました。すなわち、設計や解析の段階でばねの質量を考慮せずとも、後に簡単に修正することができるといえます。また、定性的に現象を考察する場合、ばねの質量の有無は関係なく、これまで通り質量のないばねで論ずることは妥当だといえます。

ばねの質量は1/3で効いてくる

当然といえば当然ですが、ばねの質量に対して質点の質量が大きい(\(m>>M\))場合、ばねの質量はないものとみなしてもよいと考えられます。一方で、その逆の場合には考慮しなければ影響が大きく、その影響の大きさが今回の結論より導かれたといえます。