固有振動数と共振周波数の違い

「固有振動数」や「共振」という言葉を耳にする機会があると思います。そして、ある系を固有振動数と同じ振動数で励振すると、共振し、その時の周波数を共振周波数と呼ぶとされています。しかし、これは非減衰系に対する場合に限ります。より一般的な系は減衰成分をもちますが、この時固有振動数と共振周波数の意味は異なります。ただし、固有振動数と共振周波数は近いものとなります。そのため、固有振動数と共振周波数とは等しい、もしくは近いと意味となります。

ただし、振動数$\omega$と周波数と関係は、となります。混合しないようによろしくお願いします。

本記事では、非減衰系と減衰系の強制振動を議論することで、固有振動数と共振周波数との関連を説明します。

非減衰系の強制振動
減衰系の強制振動

非減衰系の強制振動

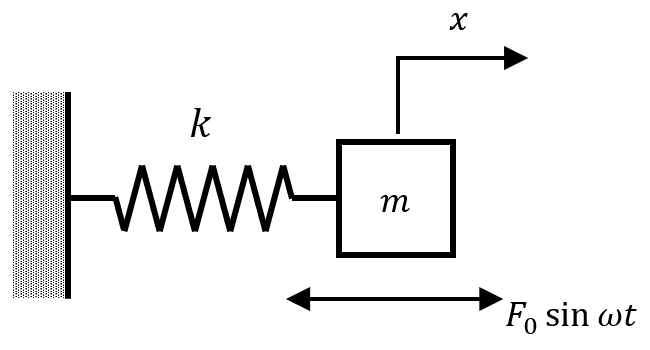
図のようなばね質量系に強制振動として振動数$\omega$の正弦波外力$f(t)=F_0\sin \omega t$を与える場合を考えます。運動方程式は、$$ m \ddot{x} + kx = F_0\sin \omega t \tag{1.1} $$となります。ここで、両辺を$m$で割り、固有振動数$\omega_n=\sqrt{k/m} $、とすれば、$$ \ddot{x} + \omega_n^2x = \displaystyle\frac{F_0}{m} \sin \omega t \tag{1.2} $$となります。また、$F_0/m$は、ばね定数$k$のばねに静的な力$F$を加えた時の静的変位なので、これを$X_s$として、$$ \ddot{x} + \omega_n^2x = X_s \sin \omega t \tag{1.3} $$となります。この微分方程式の解、つまり変位$x(t)$は、一般解(右辺=0のときの自由振動解)と特殊解との和で得られます。解くと、$$ x(t) = A\cos\omega _n t + B\sin\omega_n t + \displaystyle\frac{X_s}{1-(\omega_n/\omega)^2}\sin\omega t \tag{1.4} $$となります。ただし、定数$A$、$B$は初期条件を与えることで得られます。式(1.4)の右辺第1、2項は自由振動項、第3項は強制振動項です。ここで、強制振動の振幅$X$を静的変位$X_s$で比をとると、振幅倍率$a$は、$$ a = \displaystyle\frac{X}{X_s} = \displaystyle\frac{1}{1-(\omega_n/\omega)^2} \tag{1.5} $$となります。これを図示すると次のようになります。(式から反比例のような概形になるのは明らかだと思います。)

図からも明らかなように、$\omega = \omega_n$の時に振幅倍率は発散します。つまり、強制振動の振動数が固有振動数$\omega_n$になると共振(resonance)します。

減衰系の強制振動

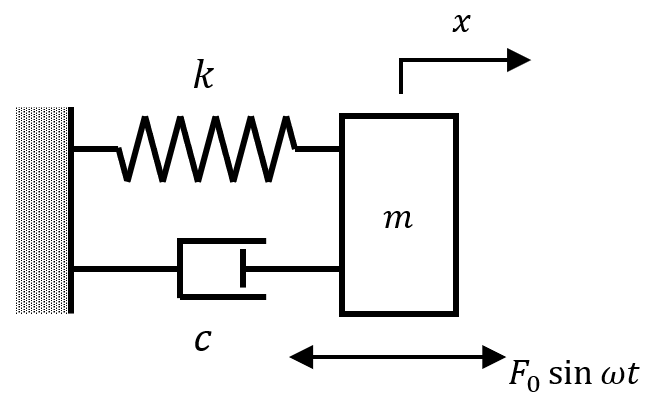
図のようなばね質量系に強制振動として振動数$\omega$の正弦波外力$f(t)=F_0\sin \omega t$を与える場合を考えます。運動方程式は、$$ m \ddot{x} + c\dot{x} + kx = F_0\sin \omega t \tag{2.1} $$となります。ここで、両辺を$m$で割り、固有振動数$\omega_n=\sqrt{k/m} $、減衰比$\zeta=c/2\sqrt{mk} $、とすれば、$$ \ddot{x} + 2\zeta\omega_n\dot{x} + \omega_n^2x = \displaystyle\frac{F_0}{m} \sin \omega t \tag{2.2} $$となります。また、$F_0/m$は、ばね定数$k$のばねに静的な力$F$を加えた時の静的変位なので、これを$X_s$として、$$ \ddot{x} + 2\zeta\omega_n\dot{x} + \omega_n^2x = X_s \sin \omega t \tag{2.3} $$となります。この微分方程式の解、つまり変位$x(t)$は、一般解(右辺=0のときの自由振動解)と特殊解との和で得られます。解くと、$$ x(t) = e^{-\zeta\omega_n t}(A\cos\omega _d t + B\sin\omega_d t) + \displaystyle\frac{X_s}{\sqrt{(1-(\omega_n/\omega)^2)^2+(2\zeta\omega_n/\omega)^2}}\sin(\omega t-\phi) \tag{2.4} $$となります。ただし、$\omega_d$($=\sqrt{1-\zeta^2}\omega_n$)は減衰固有振動数、定数$A$、$B$は初期条件を与えることで得られます。式(2.4)の右辺第1項は自由振項、第2項は強制振動項です。また、自由振動項の$e^{-\zeta\omega_n t}$は時間無限大で0に収束し、強制振動のみが残ることとなります。ここで、強制振動の振幅$X$を静的変位$X_s$で比をとると、振幅倍率$a$は、$$ a = \displaystyle\frac{X}{X_s} = \displaystyle\frac{1}{\sqrt{(1-(\omega_n/\omega)^2)^2+(2\zeta\omega_n/\omega)^2}} \tag{2.5} $$となります。これを図示すると次のようになります。(式から明らかなように、平方根の中身第2項より$\omega/\omega_n=1$では極大値をとりません。)

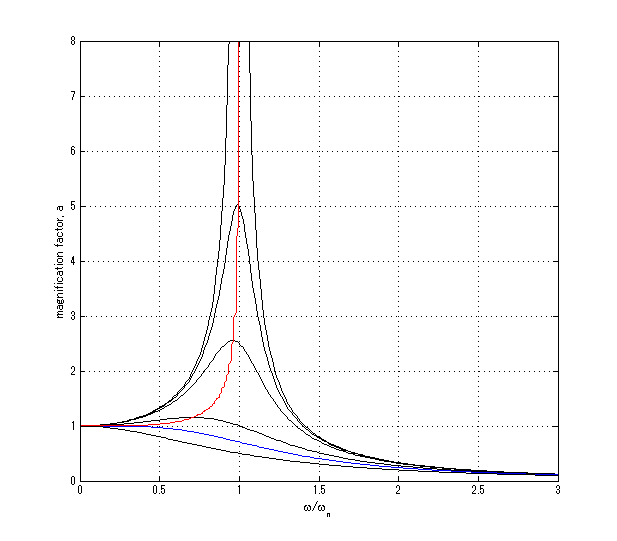
図4は、減衰比が上から$\zeta=0,0.1,0.2,0.5,1/\sqrt{2},1$のときの振幅倍率を表しています。特に青線が$\zeta=1/\sqrt{2}$であり、振幅倍率が極大値をもちうる最小の減衰比となります。また、赤線はそれぞれの減衰比における最大振幅を示したものです。つまり、減衰比が大きくなるにつれて、最大振幅となる強制振動の振動数$\omega$が小さくなっていきます。ただし、振幅倍率がある程度大きい場合における比$\omega/\omega_n$は1に近く、$\omega \approx \omega_n$であるといえます。